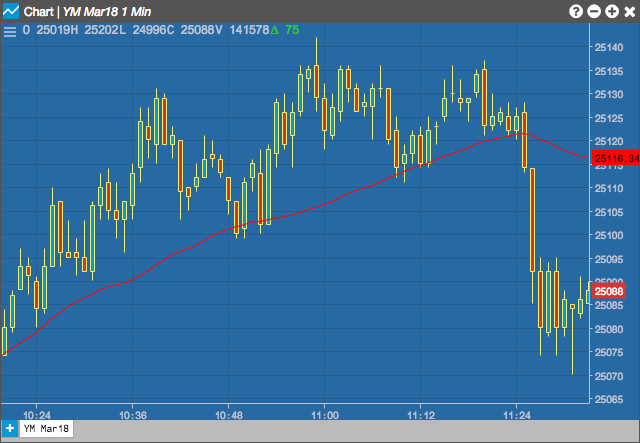
Charts
Moving Average (MA)
A moving average creates a series of averages of different subsets. Each new subset remains a constant length by adding the newest value and removing the oldest. A moving average is defined by the user over n-periods of data. This technical indicator along with several others allow the user to select which type of moving average to use in the calculation. The Formula section shows the formula for each type.
The direction of the moving average (higher, lower, or flat) indicates the trend of the market and its slope indicates the strength of the trend. Longer averages are used to identify longer-term trends while shorter averages are used to identify shorter-term trends
Configuration Options
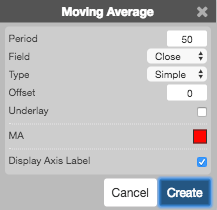
- Period: Number of bars to use in the calculations.
- Field: Price or combination of prices to use as the base for average calculations. Possible values include:
- Open
- High
- Low
- Close
- Adjusted Close
- HL/2 \( \left ( \frac{High + Low}{2} \right ) \)
- HLC/3 \( \left ( \frac{High + Low + Close}{3} \right ) \)
- HLCC/4 \( \left ( \frac{High + Low + Close + Close}{4} \right ) \)
- OHLC/4 \( \left ( \frac{Open + High + Low + Close}{4} \right ) \)
- Moving Average Type: Type of moving average to use in the calculations:
- Simple: Mean (average) of the data.
- Exponential: Newer data are weighted more heavily geometrically.
- Time Series: Calculates a linear regression trendline using the “least squares fit” method.
- Triangular: Weighted average where the middle data are given the most weight, decreasing linearly to the end points.
- Variable: An exponential moving average with a volatility index factored into the smoothing formula. The Variable Moving average uses the Chande Momentum Oscillator as the volatility index.
- VIDYA: An exponential moving average with a volatility index factored into the smoothing formula. The VIDYA moving average uses the Standard Deviation as the volatility index. (Volatility Index DYnamic Average).
- Weighted: Newer data are weighted more heavily arithmetically.
- Welles Winder:The standard exponential moving average formula converts the time period to a fraction using the formula EMA% = 2/(n + 1) where n is the number of days. For example, the EMA% for 14 days is 2/(14 days +1) = 13.3%. Wilder, however, uses an EMA% of 1/14 (1/n) which equals 7.1%. This equates to a 27-day exponential moving average using the standard formula.
- Hull: The Hull Moving Average makes a moving average more responsive while maintaining a curve smoothness. The formula for calculating this average is as follows: HMA[i] = MA( (2*MA(input, period/2) – MA(input, period)), SQRT(period)) where MA is a moving average and SQRT is square root.
- Double Exponential: The Double Exponential moving average attempts to remove the inherent lag associated to Moving Averages by placing more weight on recent values.
- Triple Exponential: TBD
- Simple
- Exponential
- Time Series
- Triangular
- Variable
- VIDYA
- Weighted
- Welles Winder
- Hull
- Double Exponential
- Triple Exponential
-
Type: Type of moving average:
- Simple: mean (average) of the data.
- Exponential: newer data are weighted more heavily geometrically.
- strong>Time Series: Calculates a linear regression trendline using the “least squares fit” method.
- Triangular: Weighted average where the middle data are given the most weight, decreasing linearly to the end points.
- Variable: An exponential moving average with a volatility index factored into the smoothing formula. The Variable Moving average uses the Chande Momentum Oscillator as the volatility index.
- VIDYA: An exponential moving average with a volatility index factored into the smoothing formula. The VIDYA moving average uses the Standard Deviation as the volatility index. (Volatility Index DYnamic Average).
- Weighted: newer data are weighted more heavily arithmetically.
- Welles Wilder: The standard exponential moving average formula converts the time period to a fraction using the formula EMA% = 2/(n + 1) where n is the number of days. For example, the EMA% for 14 days is 2/(14 days +1) = 13.3%. Wilder, however, uses an EMA% of 1/14 (1/n) which equals 7.1%. This equates to a 27-day exponential moving average using the standard formula.
- Hull
- Double Exponential
- Triple Exponential
- Offset:
- Underlay: Whether to display the moving average under the chart.
- Color Selectors: Colors to use for graph elements.
- Display Axis Label: Whether to display the most recent value on the Y axis.
Formula
\[Simple = MA = \frac{\sum_{i=1}^{n} Close_{i}}{n}\]
\[Exponential = EMA = (Close_{n} - EMA_{t-1}) \times k + EMA_{n-1}\]
where k = the smoothing constant, equal to \( \frac{2}{n+1}\)
and n = the number of periods in a simple moving average roughly approximated by the EMA
\[Time\;Series = TSMA = \frac{\sum_{i=1}^{n} Close_{i}}{n}\]
\[Triangular = TMA = \frac{\sum_{i=1}^{n} MA_{i}}{n} \]
where \(MA = \frac{\sum_{i=1}^{n} Close_{i}}{n} \)
\[Variable = VMA = \frac{P + (a \times b)P1 + {(a \times b)^2}P2 +...+{(a \times b)^{(n-1)}}P(n-1)}{1 + (a \times b) + (a \times b)^2 +...+ (a \times b)^{(n-1)}}\]
\[Weighted = WMA = \frac{n \times P + {(n-1) \times P1} + {(n-2) \times P2} +...+ P(n-1)}{1 + 2 +3 + ... +n}\]
\[Welles\;Wilder Smoothing = WWS_{n} = WWS_{n-1} - \left ( \frac{WWS_{n-1}}{n} \right )+(Value_{n})\]
where the first calculation of WWS uses a simple moving average \( WWS_{1} = \frac{\sum_{i=1}^{n} Close_{i}}{n}\)