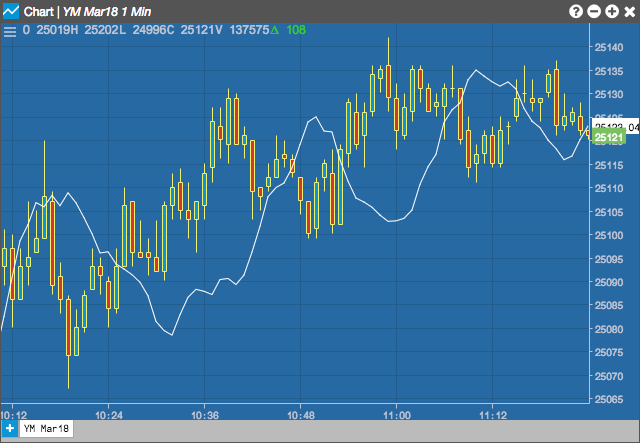
チャート
線形回帰切辺 (LRI)
線形回帰 (Linear Regression) は、過去の値から今後の値を予測するのに使用される統計ツールです。線形回帰は、価格変動時における現行トレンドの判断を、数量的に分析する方法として、一般的に使われています。線形回帰トレンドラインは、最小二乗法を用いて、価格から直線を引いたときに、その距離が最短となるように引いた線を、トレンドラインとして表示します。この線形回帰切辺 (linear regression intercept) は、各データ地点のトレンドラインの切辺を描線します。
Configuration Options
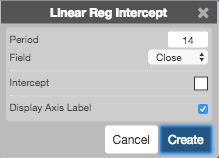
- Period (ピリオド): 計算で使用されるバー数。
- 欄: 平均計算のベースに使用する価格、または価格の組み合わせ。以下の値があります。
- Open (始値)
- High (高値)
- Low (安値)
- Close (終値)
- Adjusted Close (調整終値)
- HL/2 \( \left ( \frac{High + Low}{2} \right ) \)
- HLC/3 \( \left ( \frac{High + Low + Close}{3} \right ) \)
- HLCC/4 \( \left ( \frac{High + Low + Close + Close}{4} \right ) \)
- OHLC/4 \( \left ( \frac{Open + High + Low + Close}{4} \right ) \)
- Color Selectors (配色セレクター): グラフ要素に使用する配色。
- Display Axis Label (軸ラベルの表示): Y 軸に最新値を表示するかどうか。
数式
n 点 (x1, y1), (x2, y2), ..., (xn, yn) の最適ラインに適合する直線式は y = mx + b
\[slope\;=\;m\;=\;\frac{\sum_{i=1}^{n}(x_{i} - \bar{x})(y_{i} - \bar{y})}{\sum_{i=1}^{n}(x_{i} - \bar{x})^{2}}\]
\[intercept\;=\;b\;=\;\bar{y} - m\bar{x}\]